Começando a entender o método dos volumes finitos
O método de volumes finitos é por vezes confundido com o método das diferenças finitas pelo fato de que, em vários casos, as equações discretizadas obtidas por ambos os métodos são iguais. Entretanto, os dois métodos têm bases de formulação bastante diferentes. Enquanto o método de diferenças finitas tem uma dedução puramente matemática, a partir das aproximações de derivadas usando séries de Taylor, a formulação do método de volumes finitos tem base física.
A maioria dos modelos matemáticos utilizados em problemas de Engenharia são baseados nos princípios de conservação, que representam uma dada lei física de preservação da integridade de uma dada grandeza, ao longo de um processo. Quando um princípio de conservação é expresso de forma matemática para uma região infinitesimal de um dado meio, obtém-se uma equação diferencial, que é a chamada equação de conservação da grandeza envolvida. Por exemplo, quando se expressa matematicamente a conservação de massa no escoamento de um fluido, a equação da continuidade é obtida, que, em geometria cartesiana, é representada pela seguinte equação diferencial parcial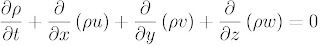 onde ρ é a densidade do fluido, t é o tempo, (x, y , z) são as três coordenadas cartesianas e (u, v , w) são as três componentes do vetor velocidade correspondentes às direções x, y e z, respectivamente. Outro exemplo pode ser dado pela equação de conservação da energia térmica para um meio fluido, originando uma das formas da equação da energia. Sob determinadas aproximações e em coordenadas cartesianas, esta equação de conservação pode ser escrita na forma abaixo
onde ρ é a densidade do fluido, t é o tempo, (x, y , z) são as três coordenadas cartesianas e (u, v , w) são as três componentes do vetor velocidade correspondentes às direções x, y e z, respectivamente. Outro exemplo pode ser dado pela equação de conservação da energia térmica para um meio fluido, originando uma das formas da equação da energia. Sob determinadas aproximações e em coordenadas cartesianas, esta equação de conservação pode ser escrita na forma abaixo
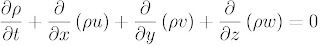 onde ρ é a densidade do fluido, t é o tempo, (x, y , z) são as três coordenadas cartesianas e (u, v , w) são as três componentes do vetor velocidade correspondentes às direções x, y e z, respectivamente. Outro exemplo pode ser dado pela equação de conservação da energia térmica para um meio fluido, originando uma das formas da equação da energia. Sob determinadas aproximações e em coordenadas cartesianas, esta equação de conservação pode ser escrita na forma abaixo
onde ρ é a densidade do fluido, t é o tempo, (x, y , z) são as três coordenadas cartesianas e (u, v , w) são as três componentes do vetor velocidade correspondentes às direções x, y e z, respectivamente. Outro exemplo pode ser dado pela equação de conservação da energia térmica para um meio fluido, originando uma das formas da equação da energia. Sob determinadas aproximações e em coordenadas cartesianas, esta equação de conservação pode ser escrita na forma abaixo onde cP é o calor específico a pressão constante, k é a condutividade térmica, T é a temperatura e Q é a taxa de geração de calor no meio por unidade de volume. A equação acima é válida para um fluido puro ou para uma mistura não-reacional, com cP constante e efeitos de compressão e dissipação viscosa desprezíveis. Maiores detalhes sobre estas e outras equações de conservação comuns aos problemas de Engenharia podem ser encontradas nos textos clássicos de Fenômenos de Transporte.
onde cP é o calor específico a pressão constante, k é a condutividade térmica, T é a temperatura e Q é a taxa de geração de calor no meio por unidade de volume. A equação acima é válida para um fluido puro ou para uma mistura não-reacional, com cP constante e efeitos de compressão e dissipação viscosa desprezíveis. Maiores detalhes sobre estas e outras equações de conservação comuns aos problemas de Engenharia podem ser encontradas nos textos clássicos de Fenômenos de Transporte.Em geral, as equações de conservação apresentam termos que representam o acúmulo, o transporte convectivo, o transporte difusivo e a geração de uma dada grandeza. Veja, por exemplo, a equação da energia. O primeiro termo do membro esquerdo é o termo de acúmulo, enquanto que os outros termos deste lado da equação são termos de transporte por convecção. No membro direito da equação da energia, os três primeiros termos correspondem ao transporte difusivo, sendo o último o termo de geração. Por esta similaridade, as equações de conservação podem ser escritas na seguinte forma geral
 onde φ é a grandeza conservada, Γ é a difusividade desta grandeza e S é o termo de geração. Note que esta equação generalizada é válida também para outros sistemas de coordenadas além do cartesiano, bastando para isto interpretar as variáveis (x, y , z) como sendo as coordenadas do outro sistema, e considerando S como sendo a soma do termo de geração com todos os outros termos existentes na equação de conservação original que não se enquadram nem na forma de termos de transporte e nem na de termo de acúmulo. Por isso, o termo S é, por vezes, chamado de "lixeira" da equação de conservação, na forma dada acima.
onde φ é a grandeza conservada, Γ é a difusividade desta grandeza e S é o termo de geração. Note que esta equação generalizada é válida também para outros sistemas de coordenadas além do cartesiano, bastando para isto interpretar as variáveis (x, y , z) como sendo as coordenadas do outro sistema, e considerando S como sendo a soma do termo de geração com todos os outros termos existentes na equação de conservação original que não se enquadram nem na forma de termos de transporte e nem na de termo de acúmulo. Por isso, o termo S é, por vezes, chamado de "lixeira" da equação de conservação, na forma dada acima.Esta forma para a equação de conservação é chamada de forma conservativa ou forma divergente, na qual os termos relativos aos fluxos convectivos, ρuφ, ρvφ e ρwφ, aparecem dentro das derivadas em relação às coordenadas espaciais, x, y , z. Qualquer outra forma é dita não-conservativa. A forma conservativa é a forma da equação obtida diretamente da forma integral da lei de conservação. Por exemplo, considere a equação da continuidade, cuja forma integral, válida para um volume finito fixo no espaço, é dada por

onde v é o vetor velocidade, de componentes (u, v , w), V é o volume finito no qual a conservação de massa está sendo aplicada, A é a superfície deste volume, n é o vetor unitário normal externo à superfície A e o ponto entre o vetor velocidade e o vetor normal à superfície indica o produto escalar. De fato, esta equação diz, simplesmente, que a variação da massa contida no volume é causada pela taxa líquida de massa que é transferida através da superfície do corpo.
Utilizando o teorema integral de Gauss (ou da divergência), que pode ser encontrado nas referências clássicas de Fenômenos de Transporte, a equação acima pode ser escrita na forma

onde ∇· (ρv) é o divergente do fluxo mássico que, em geometria cartesiana, é expresso por

A equação acima é válida para qualquer volume V , de forma que o integrando deve ser nulo, o que origina a equação diferencial parcial na forma conservativa, dada pela primeira equação.
Na minha opinião, um bom conhecimento da equação de conservação é a primeira etapa para entender o método dos volumes finitos. No próximo post, vou abordar os princípios da discretização da equação de conservação pelo método dos volumes finitos.
Um abraço e até a próxima.
Referências:
[1] Apostila e notas de Aula do curso de mestrado de Fluidodinâmica Computacional (PEQ/COPPE/UFRJ).


Excelente post, bem simplificado e fácil de entender.
ReplyDelete