Análise de código no OpenFOAM - laplacianFoam

Para explicar a estrutura e o algoritmo de solução de um código no OpenFOAM, vou usar como base o solver laplacianFoam. Para acompanhar melhor esse post, é interessante que o leitor tenha alguns conhecimentos básicos da sintaxe de C++. Porém, vou apresentar alguns detalhes referentes aos comandos e funções que são membros das classes e templates, facilitando a leitura do código para os leitores sem experiência em linguagens orientadas a objetos.

O solver laplacianFoam é usado para resolver o problema da difusão pura de um campo escalar T, sem considerar nenhum termo fonte. Esta equação está colocada abaixo, sendo D o coeficiente de difusão.

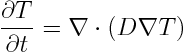
Os arquivos referentes aos solvers do OpenFOAM ficam no diretório OpenFOAM-version/applications/solvers., onde version se refere a versão do OpenFOAM. O código do laplacianFoam fica no diretório basic e está colocado abaixo.

00001 /*---------------------------------------------------------------------------*\
00002   =========                 |
00003   \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox
00004    \\    /   O peration     |
00005     \\  /    A nd           | Copyright (C) 1991-2008 OpenCFD Ltd.
00006      \\/     M anipulation  |
00007 -------------------------------------------------------------------------------
00008 License
00009     This file is part of OpenFOAM.
00010 
00011     OpenFOAM is free software; you can redistribute it and/or modify it
00012     under the terms of the GNU General Public License as published by the
00013     Free Software Foundation; either version 2 of the License, or (at your
00014     option) any later version.
00015 
00016     OpenFOAM is distributed in the hope that it will be useful, but WITHOUT
00017     ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
00018     FITNESS FOR A PARTICULAR PURPOSE.  See the GNU General Public License
00019     for more details.
00020 
00021     You should have received a copy of the GNU General Public License
00022     along with OpenFOAM; if not, write to the Free Software Foundation,
00023     Inc., 51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA
00024 
00025 Application
00026     laplacianFoam
00027 
00028 Description
00029     Solves a simple Laplace equation, e.g. for thermal diffusion in a solid.
00030 
00031 \*---------------------------------------------------------------------------*/
00032
00033 #include "fvCFD.H"
00034
00035
00036 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
00037
00038 int main(int argc, char *argv[])
00039 {
00040
00041 #   include "setRootCase.H"
00042
00043 #   include "createTime.H"
00044 #   include "createMesh.H"
00045 #   include "createFields.H"
00046
00047 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
00048
00049     Info<< "\nCalculating temperature distribution\n" << endl;
00050
00051     for (runTime++; !runTime.end(); runTime++)
00052     {
00053         Info<< "Time = " << runTime.timeName() << nl << endl;
00055 #       include "readSIMPLEControls.H"
00056
00057         for (int nonOrth=0; nonOrth<=nNonOrthCorr; nonOrth++)
00058         {
00059             solve
00060             (
00061                 fvm::ddt(T) - fvm::laplacian(DT, T)
00062             );
00063         }
00064
00065 #       include "write.H"
00066
00067         Info<< "ExecutionTime = " << runTime.elapsedCpuTime() <<" s"
00068             << "  ClockTime = " << runTime.elapsedClockTime() <<" s"
00069             << nl << endl;
00070     }
00071
00072     Info<< "End\n" << endl;
00074     return(0);
00075 }
00076
00077
00078 // ************************************************************************* //

Para acompanhar a leitura, sugiro que você abra diretamente o arquivo laplacianFoam.C em um editor de textos de sua preferência. De forma mais direta, você também acessar o código do laplacianFoam abrindo este link em uma outra aba do seu navegador.

A primeira linha a ser executada no código (linha 33) declara a biblioteca fvCFD.H, que fornece ao solver acesso a todas as classes e propriedades descritas em meu post anterior. Deve-se frisar que é vital declarar esta biblioteca. Na linha 38, a função main engloba todo o código fonte principal e possui dois argumentos de entrada: o inteiro argc e a cadeia de caracteres argv. Estes parâmetros contém informações sobre a simulação, como o diretório e o nome do caso a ser simulado. Os argumentos são lidos pelo programa diretamente na linha de comando para execução do solver.

A biblioteca setRootCase.H é usada para testar a validade dos argumentos argc e argv da simulação. O conteúdo desta biblioteca está colocado abaixo.

00001 Foam::argList args(argc, argv);
00002
00003 if (!args.checkRootCase())
00004 {
00005     Foam::FatalError.exit();
00006 }

O primeiro comando do código acima declara a variável args construída com os argumentos argc e argv, a partir da classe argList. Em seguida, o comando checkRootCase() verifica a validade e a existência do diretório e do nome do caso simulado. Caso o retorno de checkRootCase() seja False, a execução do solver é interrompida pelo comando padrão de erro do OpenFOAM FatalError.

As duas próximas bibliotecas declaradas, createTime.H e createMesh.H, são responsáveis pela criação de bancos de dados para armazenar dados sobre o caso simulado e a estrutura da malha utilizada. O código colocado abaixo refere-se à biblioteca createTime.H.

00001     Foam::Info<< "Create time\n" << Foam::endl;
00002
00003     Foam::Time runTime
00004     (
00005         Foam::Time::controlDictName,
00006         args.rootPath(),
00007         args.caseName()
00008     );

Sendo construída a partir de informações sobre o nome e o diretório do caso simulado (provindas de args), a variável runTime do template Time é declarada no código acima. Desta forma, runTime obtém a localização do arquivo de configuração controlDict do caso e, utilizando as informações contidas neste último, monta um banco de dados para controle da simulação. Por exemplo, pode-se citar alguns dos dados contidos em runTime: (i) instante inicial e final; (ii) controle do passo de tempo (fixo, adaptativo, etc.); (iii) diretórios que contém os arquivos com os campos iniciais das propriedades transportadas; (iv) controle de escrita em arquivo (formato de saída, compressão de dados, etc.); entre outros.

A biblioteca createMesh.H usa o template fvMesh para declarar a variável mesh, construída a partir de outro template chamado IOobject, como mostra o código a seguir.

00001     Foam::Info<< "Create mesh for time = "
00002         << runTime.timeName()<< Foam::nl << Foam::endl;
00003
00004     Foam::fvMesh mesh
00005     (
00006         Foam::IOobject
00007         (
00008             Foam::fvMesh::defaultRegion,
00009             runTime.timeName(),
00010             runTime,
00011             Foam::IOobject::MUST_READ
00012         )
00013     );

O template IOobject define os atributos de um objeto de modo a fornecer meios para entrada e/ou saída de dados (usualmente em arquivo). Com as informações de runTime, o template fvMesh é capaz de localizar os arquivos cells, faces, points e boundary para construção da malha. Note que o último parâmetro na construção de IOobject refere-se à regras de leitura e escrita de arquivos. Neste caso, a leitura dos dados deve ser obrigatória (MUST_READ).

Todas as bibliotecas supracitadas são gerais e podem ser usadas em qualquer código do OpenFOAM (salvo pequenas modificações já comentadas). Contudo, a biblioteca createFields.H é usada para criação e leitura dos campos iniciais das incógnitas do problema e leitura de propriedades físicas aplicadas a cada caso (propriedades de transporte, termodinâmicas, termofísicas, etc.). Desta forma, este header é específico para cada solver e deve ser desenvolvido com cuidado pelo programador, pois todas as incógnitas e todas as propriedades físicas do problema devem ser definidas neste arquivo. Portanto, deve-se ter domínio do modelo fluidodinâmico e qual a melhor forma de armazenar suas variáveis de modo a otimizar o código. A biblioteca createFields.H específica para o laplacianFoam está colocada abaixo.

00001     Info<< "Reading field T\n" << endl;
00002
00003     volScalarField T
00004     (
00005         IOobject
00006         (
00007             "T",
00008             runTime.timeName(),
00009             mesh,
00010             IOobject::MUST_READ,
00011             IOobject::AUTO_WRITE
00012         ),
00013         mesh
00014     );
00015
00016
00017     Info<< "Reading transportProperties\n" << endl;
00018
00019     IOdictionary transportProperties
00020     (
00021         IOobject
00022         (
00023             "transportProperties",
00024             runTime.constant(),
00025             mesh,
00026             IOobject::MUST_READ,
00027             IOobject::NO_WRITE
00028         )
00029     );
00030
00031
00032     Info<< "Reading diffusivity DT\n" << name="l00033">00033
00034     dimensionedScalar DT
00035     (
00036         transportProperties.lookup("DT")
00037     );

Para resolver o problema, a temperatura deve ser definida em um campo geométrico (template geometricField). Fisicamente, a temperatura é uma variável escalar e, portanto, deve-se criar um campo geométrico de um escalar. O template volScalarField constrói um campo escalar da variável T, definida no centro das células da malha mesh. A criação deste campo depende dos templates IOobject e fvMesh como argumentos de entrada. O primeiro constrói o objeto, definindo o nome da variável e do arquivo que contém os valores do campo inicial de T (O nome do arquivo que contém o campo inicial da variável é idêntico ao nome da própria variável), o registro das informações contidas em runTime (por exemplo, o diretório e a periodicidade da saída de resultados em arquivo) e as opções de entrada e saída de dados (MUST_READ indica que o campo inicial de T deve ser necessariamente lido e AUTO_WRITE configura a saída automática de T em arquivo ao longo do tempo). O segundo parâmetro para a criação de T é o template fvMesh definido como mesh, que indica onde o campo escalar T será alocado e inserido.

A equação da difusão possui apenas uma propriedade física de transporte, a condutividade térmica DT (representada pela letra D na equação da difusão). A leitura das propriedades de transporte é realizada através do template IOdictionary, construída a partir do template IOobject como argumento. O template IOdictionary, por sua vez, é derivada de outros dois templates, dictionary e IOobject, proporcionando funcionalidade na entrada e saída de dados automática a partir de um banco de dados. O template dictionary define uma lista de palavras chave, onde cada uma destas é associada a um número arbitrário de valores. A construção de transportProperties declara o nome do arquivo que contém as propriedades de transporte e seu diretório (runTime.constant()) e as regras de leitura (MUST_READ) e saída (NO_WRITE) de dados em arquivo. Por fim, a criação da variável escalar dimensional DT é construída pelo comando transportProperties.lookup("DT"), que procura no arquivo transportProperties a palavra-chave "DT" e associa um valor dimensional a essa variável.

As etapas descritas acima apenas inicializam os dados para runTime, a malha mesh, o campo inicial de T e a propriedade de transporte DT do código principal. O próximo passo é programar o algoritmo de solução do problema específico.

O laço for, iniciado na linha 51 do código principal, tem o intuito de repetir as instruções no interior do laço para cada passo de tempo (incrementado por runTime++). O laço é realizado até que a condição de runTime.end() seja satisfeita (retorne true).

O primeiro comando no interior do laço é a declaração do header readSIMPLEControls.H para leitura dos parâmetros do método SIMPLE de acoplamento pressão-velocidade e das condições de ortogonalidade da malha. Estes parâmetros são lidos no arquivo fvSolution do caso analisado. Apesar de não ser necessário aplicar o método SIMPLE para resolver a equação da difusão pura, esta biblioteca lê o número de iterações para correção dos fluxos devido à não-ortogonalidade da malha. Isso é necessário pois o OpenFOAM divide o cálculo do fluxo através das faces em duas parcelas chamadas contribuição ortogonal e a correção não ortogonal. Esta correção é realizada um laço para ajustar o fluxo das propriedades nas faces dos volumes, semelhante ao esquema defferred correction. Maiores detalhes podem ser encontrados na tese do Prof. Jasak.

A discretização por volumes finitos é realizada pelo template fvm, armazenando as equações discretizadas em sua forma matricial com o template fvMatrix e montando um sistema de equações lineares resolvido pelo comando solve. Este último comando retorna na tela para o usuário dados estatísticos da solução, como a convergência do sistema, número de iterações, etc. A definição das formulações de discretização usadas na simulação estão colocadas no arquivo fvShemes. A solução do sistema algébrico, cujo método de solução está selecionado no arquivo fvSolution, retorna a temperatura em cada célula da malha. A biblioteca write.H, colocada abaixo, escreve os arquivos de resultados quando o comando de classe runTime.output() for válido.

00001     if (runTime.outputTime())
00002     {
00003         volVectorField gradT = fvc::grad(T);
00004
00005         volScalarField gradTx
00006         (
00007             IOobject
00008             (
00009                 "gradTx",
00010                 runTime.timeName(),
00011                 mesh,
00012                 IOobject::NO_READ,
00013                 IOobject::AUTO_WRITE
00014             ),
00015             gradT.component(vector::X)
00016         );
00017
00018         volScalarField gradTy
00019         (
00020             IOobject
00021             (
00022                 "gradTy",
00023                 runTime.timeName(),
00024                 mesh,
00025                 IOobject::NO_READ,
00026                 IOobject::AUTO_WRITE
00027             ),
00028             gradT.component(vector::Y)
00029         );
00030
00031         volScalarField gradTz
00032         (
00033             IOobject
00034             (
00035                 "gradTz",
00036                 runTime.timeName(),
00037                 mesh,
00038                 IOobject::NO_READ,
00039                 IOobject::AUTO_WRITE
00040             ),
00041             gradT.component(vector::Z)
00042         );
00043
00044
00045         runTime.write();
00046     }

Com o intuito de também escrever em arquivo os componentes do gradiente da temperatura, calcula-se gradT pela classe fvc que realiza operações tensoriais explícitas com os dados da malha. Note que, como a temperatura é uma variável escalar, seu gradiente será uma entidade vetorial, e portanto o tipo da variável gradT deve ser um volVectorField. As linhas 5, 18 e 31 do código acima decompõem gradT nas direções X, Y e Z do domínio e definem esta variável como AUTO_WRITE para que a saída em arquivo seja automática. Cada decomposição é, portanto, um volScalarField e será formado pela componente do vetor de gradT da respectiva direção. O comando runTime.write() escreve em arquivos os valores de temperatura nos centros das células, seus gradientes e os componentes do gradiente.

O algoritmo repete-se até o fim do laço no tempo e, por consequência, o final da simulação. Na minha opinião, o solver laplacianFoam possui o código mais simples de todos. A complexidade dos códigos aumenta junto com o detalhamento dos fenômenos físicos considerados, sendo necessário o desenvolvimento de algoritmos mais elaborados, o uso de mais templates, classes e comandos.

Espero que este post seja de ajuda aos que estão começando a estudar e desbravar a programação no OpenFOAM. Se quiserem discutir mais sobre o assunto ou mesmo trocar idéias, deixe um comentário aqui.

Um abraço!